ずばり以下の式です。(有名な式かもしれないですが、習った記憶はありません。)
例として、n = 5のときを考えてみます。 1 - 5 + 10 - 10 + 5 - 1 = 0なので確かに上式が成り立ちます。ついでにn=4のときもやってみます。1 - 4 + 6 - 4 + 1 = 0でやはり成り立ちます。
パスカルの三角形を書くと、一般のnについて確かにそうなってるなというのが分かります。
まずnが奇数のときを考えてみます。nが奇数のときは左辺の項数がn+1で偶数個になります。+の項と-の項に分けて考えると、
+ - + - + - + -
のようになります。ここで、
を使うと、+と-の項がいいかんじに打ち消しあって和が0になるのが分かります。
次にnが偶数のときを考えます。このときは、パスカルの三角形において自分の値 = 上の2つの値の和
となっているのを利用します。これを利用すると隣合う項同士が消去しあって和が0になるのが分かります。
二項係数といえば以下の式が有名ですが、今回出会った式もなかなかの美式だなぁと思います。
%5E%7Bk%7D%20%5Cbinom%7Bn%7D%7Bk%7D%20%3D%200.png)
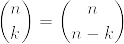
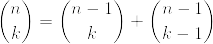
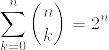
(1-1)^nの二項展開に他ならないので自明ですね
返信削除