メルセンヌ素数と完全数には面白い関係がある。
1. メルセンヌ素数とは?
メルセンヌ素数とは、メルセンヌ数かつ素数であるような数のこと。メルセンヌ数とは、2k-1という形で表される数のことで、2進数で表したときに、1のみで構成される数のことである。
2. 完全数とは?
完全数とは、その数のproper divisor(自分以外の約数)の和が自分自身と等しいような数のこと。
6 = 1 + 2+ 3
28 = 1 + 2 + 4 + 7 + 14
が最初の2つの完全数である。
3. 面白い関係って?
メルセンヌ素数と完全数の間には以下の定理が成り立つ。
メルセンヌ数2
k-1が素数であるとき、2
k-1(2
k-1)は完全数である。逆に、すべての偶数の完全数は、2
k-1(2
k-1)という形(2の冪乗とメルセンヌ素数の積)で表現できる。(※
注意)
証明のために関数σを導入します。σ(n)は、nの約数(properな約数ではなく、自分自身も含むことに注意)の和を表します。例えば、
σ(6) = 1 + 2 + 3 + 6 = 12
です。nが完全数の場合は、σ(n) = 2nです。
この関数σについて以下の補題を考えます。
N = ab(a, bは互いに素)と表せるとき、σ(N) = σ(a) * σ(b)である。
証明) σ(a) * σ(b) = (a1 + a2 + a3 + ... ) * (b1 + b2 + b3 + ... ) = Σ(aの約数 * bの約数)である。ここでa1,a2,..はaの約数、b1,b2,..はbの約数である。よって、(aの約数 * bの約数)がNの約数となることと、Nの任意の約数dがある一組の(i, j)についてd = ai * bjとなることを示せばよい。
まず前半だが、a, bが互いに素であるため、a x + b y = 1となるような整数(x, y)が存在する。両辺にNをかけると、a x N + b y N = Nとなる。aの約数 | a かつ bの約数 | Nなので、(aの約数 * bの約数)はa x Nを割りきる。同様に(aの約数 * bの約数)はb y Nを割りきる。よって(aの約数 * bの約数)はNを割りきる。
次に後半を示す。a, bの素因数分解を
a = p1k1p2k2p3k3...pnkn
b = q1t1q2t2q3t3...qmtm
と表記する。ki > 0, i = 1,2,...n、およびtj > 0, j = 1,2,..mである。また、aとbが互いに素なので、pi≒qj, i=1,2,..n, j =1,2,...mである。
N= a * bなので、Nの素因数分解は
N = p1k1p2k2p3k3...pnkn q1t1q2t2q3t3...qmtm
となる。ここで、Nの任意の約数は、
x = p1k'1p2k'2p3k'3...pnk'n q1t'1q2t'2q3t'3...qmt'm
と表すことができる。ただし、0 ≦k'i ≦ki, i = 1,2,...n、0 ≦ t'j ≦tj, j=1,2,...,m.である。
Nの任意の約数を選ぶことと、(k'1,k'2, ..., k'n, t'1,t'2,..., t'm)の値を決めることは一対一に対応している。(k'1,k'2, ..., k'n, t'1,t'2,..., t'm)が決まれば、(k'1,k'2, ..., k'n)、(t'1,t'2,..., t'm)が決まり、これは、対応するaの約数、bの約数が一意に決まることを意味する。□
それでは、メルセンヌ素数と完全数に関する定理の証明に入ります。まず、最初の部分を証明します。
2k-1は素数なので、σ(2k-1) = 1 + 2k-1 = 2kです。2k-1は、2のべき乗なので約数は1, 2, 22, .... 2k-2, 2k-1である。よって、σ(2k-1) = 1 + 2 + 22 + ... + 2k-1 = 2k-1。2k-1(2の冪乗)と2k-1(奇数)は互いに素なので補題より、σ(2k-1(2k-1)) = σ(2k-1) * σ(2k-1) = (2k-1) * 2k = 2 * 2k-1(2k-1)となる。
σ(n) = 2nなので、2k-1(2k-1)は完全数である。
次に後半を示す。偶数の完全数を2k-1mと表記する。ただし、k≧2、mは奇数。
補題よりσ(2k-1m) = σ(2k-1) * σ(m) = (2k-1) σ(m)。
また、2k-1mは完全数であることから、σ(2k-1m) = 2 * 2k-1m = 2km。
よって、
2km = (2k-1) σ(m)。
ここで、(2k-1) | 2km、かつ2kと(2k-1)は互いに素であることから、(2k-1) | m。
よって、m = (2k-1) Mとして先ほどの式に代入すると
2k (2k-1) M = (2k-1) σ(m)となり、両辺を (2k-1) で割ると、
2kM = σ(m)。
m + M = (2k-1) M + M = 2kMより、σ(m) = m + Mとなるが、これはmが素数で、M=1であることを意味する。よって、m = 2k-1(素数)となり、もともとの完全数は、2k-1(2k-1)と表される。□
(※注意)奇数の完全数が存在するか否かは不明です。現時点で発見されている完全数はすべて偶数です。
参考:




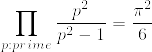
%7D.png)
%20%3D%20%5Cprod_%7Bp%20:%20prime%7D%20%5Cfrac%7Bp%5Ex%7D%7Bp%5Ex%20-%201%7D.png)



%20%3D%20%5Cfrac%7B1%7D%7B2%5Cpi%7D%5Cexp%5Cleft(%5Cfrac%7Bx%5E2%20+%20y%5E2%7D%7B2%7D%5Cright).png)






