エルミート行列はグラフ理論(無向グラフの隣接行列はエルミート行列)とか解析学(二次形式の行列表現、二階偏微分が連続な場合のヘッセ行列はエルミート行列)とかその他もろもろに応用できそうなので、まずは基本からしっかり抑えたい。
証明
複素数の内積についていろいろ忘れていたので、そこから復習した。まず複素ベクトルの内積の定義。(以下ではx, yともにn次元複素ベクトルとする。)
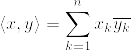
実数ベクトルのときと違って、内積はcommutativeじゃない。
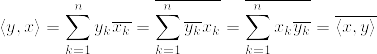
スカラー倍したときも、実数ベクトルとは少し違う。
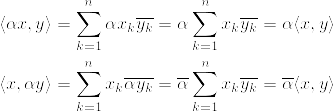
じぇ!
それから以下のような性質が成り立つ(証明略。両辺を展開すると等しいことが分かる)。
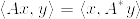
複素ベクトルについてはこのあたりにしておいて、エルミート行列の固有値の話に戻る。
エルミート行列Aの固有値をλ, 対応する固有ベクトルをvとする。(Av = λv)
上で復習した複素ベクトルの内積に関する性質を使って式変形していくと、
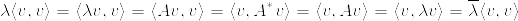
が成り立つ。
ここで、vは固有ベクトルなので|v| != 0. よって両辺を|v|で割るとλ = (λの共役複素数)となる。つまりλは実数となる。□
確認
いくつかの例について確認してみた。
まずは実対称行列の場合。
>>> import numpy as np >>> A = np.matrix([ ... [4, -2], ... [-2, 1] ... ]) >>> eval, evec = np.linalg.eig(A) >>> eval array([ 5.00000000e+00, -1.08420217e-19])
固有値は実数になってる。この場合は見ただけで分かるか。
det(A) = 0なので、固有値の1つは0。
tr(A) = 5なので、もう1つの固有値は5。
という具合に。
次に3*3のエルミート行列。
>>> A = np.matrix([
... [2, 3+1j, -5j],
... [3-1j, -4, -6+11j],
... [5j, -6-11j, 1]
... ])
>>> eval, evec = np.linalg.eig(A)
>>> eval
array([-15.79791935 -1.51076040e-16j, 2.60643760 -1.56021493e-16j,
12.19148175 +1.55092389e-16j])
全部実数になってる。じぇじぇじぇ!
参考URL
[1] http://people.math.gatech.edu/~meyer/MA6701/module11.pdf
0 件のコメント:
コメントを投稿