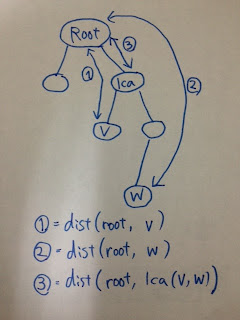
頂点v, w間の距離を求めたい場合は、dist(v, w) = dist(root, v) + dist(root, w) - 2 * dist(root, lca(v, w))となる。
以下に簡単な練習問題がある。
http://poj.org/problem?id=1986
ACしたソースコード。
#include <vector> #include <cstdio> using namespace std; vector<pair<int, int> > G[40000]; class LCA { public: int V, logV; vector<int> depth, len; vector<vector<int> > parent; LCA(int V) { this->V = V; logV = 0; while (V > (1LL<<logV)) logV++; this->depth = vector<int>(V); this->len = vector<int>(V); this->parent = vector<vector<int> >(logV, vector<int>(V)); } void init(int v, int par, int d, int l) { depth[v] = d; parent[0][v] = par; len[v] = l; for (int i = 0; i < (int)G[v].size(); i++) { int w = G[v][i].first; int lc = G[v][i].second; if (w == par) continue; init(w, v, d+1, lc + l); } } void build() { for (int k = 0; k + 1 < logV; k++) { for (int v = 0; v < V; v++) { if (parent[k][v] < 0) parent[k+1][v] = -1; else parent[k+1][v] = parent[k][parent[k][v]]; } } } int query(int u, int v) { if (depth[u] > depth[v]) swap(u, v); for (int k = 0; k < logV; k++) { if ((depth[v] - depth[u]) >> k & 1) v = parent[k][v]; } if (u == v) return u; for (int k = logV-1; k >= 0; k--) { if (parent[k][u] != parent[k][v]) { u = parent[k][u]; v = parent[k][v]; } } return parent[0][u]; } }; int main(int argc, char **argv) { int N, M; scanf("%d %d", &N, &M); for (int i = 0; i < M; i++) { int x, y, len; char c; scanf("%d %d %d %c", &x, &y, &len, &c); --x, --y; G[x].push_back(make_pair(y, len)); G[y].push_back(make_pair(x, len)); } LCA lca(N); lca.init(0, -1, 0, 0); lca.build(); int Q; scanf("%d", &Q); while (Q--) { int x, y; scanf("%d %d", &x, &y); int z = lca.query(--x, --y); int ret = lca.len[x] + lca.len[y] - 2 * lca.len[z]; printf("%d\n", ret); } return 0; }
0 件のコメント:
コメントを投稿