FFTでconvolutionするときのサンプリング数

Hacker CupのScott's New Trickという問題を復習していて、ちょっとはまったのでメモ。

（昔解いたときはここまで分かっていたのだろうか。）

どこではまったかというと、FFTするときに点の数をいくつにするべきかということ。十分に大きな2のべき乗をとればいいんだけど、”十分大きな”がいまいち分かってなかった。

まず抑えておかないといけないのは、FFTでconvolutionを計算したときにえられる値と、実際に計算したい値が異なるということ。

上に書いているようにFFTで計算されるz[k]はNを法としたときにi + j = kとなるようなx[i] * y[j]の和になる。でもこの問題で計算したいのは、原始根gのべき乗の周期である(P-1)を法としたときにi + j = kとなるようなx[i] * y[j]の和である。以下の例で説明するように、Nの選択を誤ってしまうと実際に欲しい値が計算できなくなってしまう。

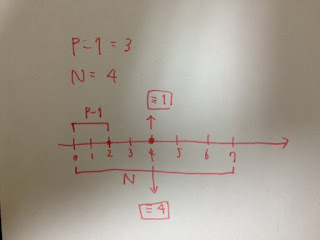
もし、(P-1) < Nとなるような最小のNをとったとする。たとえばP-1 = 3、N = 4とする。

法P-1の世界における代表元は{0, 1, 2}、法Nの世界における代表元は{0, 1, 2, 3}となる。このときconvolutionの中に含まれるx[2] * y[2]がどうなるかを考えてみる。FFTをすると、法Nの世界では2 + 2 = 0なので、z[0]の和に足される。でも法(P-1)の世界では2 + 2 = 1なので、これはz[1]に足されていて欲しい。

というふうになってズレが生じてしまう。

2 * (P-1) < NとなるようなNをとってみる。P-1 = 3に対して、N = 8としてみる。

このとき、x[2] * y[2]はz[4]に足されることになる。FFTが終わったあとで、改めてz[1] := z[1 + k * (P-1)]のように定義しなおせば欲しい値を矛盾無く計算できる。

以上をふまえると、P-1については、2 * (P-2) < NとなるようなNをFFTの点の数に選べばいいということになる。大学のときにサンプルリング定理（最大周波数の２倍以上の点でサンプリングしないと元の信号を復元できない）っていうのを習った記憶があるけど、それと同じような感じかな。

コンテストで同様の問題が出た場合は、while (N < P) N <<= 1; N <<= 1; ぐらいに書いておけばいいってことか。