群構造とラテン方格

気になっていた群の性質

　群のoperation tableを見ていてずっと気に成っていたことがありました。ちょうどそれに関する証明問題があったので解いてみました。

For any two elements x and y in G, there is an element z in G such that y = xz.

　上の内容は0以外の実数集合と乗算演算からなる群<R^*, ・>の場合、あたり前のことを言っています。任意の実数x, yについて、z = y/x とすれば、y = xzが成り立ちます。この関係が有限群でも成り立つのかどうかは興味深いです。これまでいくつかの群構造を見てきましたが、そのすべてにおいて上の関係が成り立っていました。

　

　以下考えた証明です。

　Let x be an element in G.

Apply the operator to x with all the elements in G, namely x₁, x₂, .... x_n.

xx₁, xx₂, ....., xx_n　　　(1)

　Since G is closed with respect to the operation, all the above results are belong to G.

If xx_i = xx_j, by canceling x from the both sides, x_i = x_j.So if x_i ≠ x_j, then xx_i ≠ xx_j holds.

　Therefore, it comes down to that (1) is a permutation of x₁, x₂, ....., x_n,

which follows that for any x and y G, there is an element z such that y = xz.

ラテン方格とは？

　証明を考えているときに、これってラテン方格だよなーと思って調べてみました。ラテン方格とは、n*nの格子でどの列を見てもどの行を見ても[1, n]の値が1回ずつ出てくるような格子です。

　

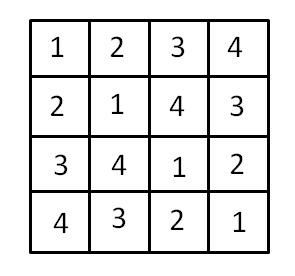
群構造とラテン方格の関係

群構造を持つ代数系のoperation tableを書くとラテン方格になります。上の証明で行に関してはpermutationになっていることを示しています。列に関しても同様に示すことができます。

　ここでもう一つ疑問がわきました。「operation tableがラテン方格になるように演算を定義すれば、それは必ず群になるのか？」ということです。wikipediaのページに反例が載ってました。

operation tableがラテン方格でも、必ずしも群にはならないようです。この群のようで群じゃない代数構造をquasigroup（日本語だと準群??）と呼ぶそうです。また、identity elementを持つ quasigroup をloopと呼ぶそうです。

２要素集合上でassociativeな演算

集合X = {0, 1}上で閉じた任意の二項演算*を考えます。関数の入力パターンは2*2=4通り、その4通りの入力それぞれについて2通りの出力を考えることができるので全部で2⁴ = 16通りの演算を考えることができます。

例えば以下のような演算を定義することができます。いわゆるAND演算です。

a	b	a * b
0	0	0
0	1	0
1	0	0
1	1	1

　ここで「考えうる16パターンすべての演算についてassociativeな演算はいくつあるのか?」という興味が湧いてきました。associativeな演算とは、すべてのa, b, c ∈ Xについて(a * b) * c = a * (b * c)をみたす演算です。それぞれの関数につき2*2*2=8通りの入力パターンすべてを手で検証するのは大変なので、コンピュータの力を借りることにしました。

　今回は集合の要素が0, 1なので二進数を使うと上手くコーディングができそうです。0*0の結果を0ビット目に、0*1の結果を1ビット目に・・・のように格納すると4ビットのビット列で演算を一意に表すことができます。例えば、上記のANDなら"1000"です。あとは、このビット列をどう関数と結び付けるかです。

　C++では関数オブジェクト(functor)を利用することでクロージャのようなものが実現できるので、それを利用します。以下のソースでは、関数オブジェクトfは生成時に与えられたビット列に対応した入出力機構を持つ関数のようにふるまいます。

class Functor {
    int mask;
public:
    Functor (int mask) {
        this->mask = mask;
    }

    int operator()(int a, int b) {
        return mask >> (a << 1 | b) & 1;
    }
};

int main() {
    for (int k = 0; k < 1<<4; k++) {
        Functor f(k);

        bool ck = true;
        for (int x = 0; x <= 1; x++) {
            for (int y = 0; y <= 1; y++) {
                for (int z = 0; z <= 1; z++) {
                    if (f(x, f(y, z)) != f(f(x, y), z)) {
                        ck = false;
                    }
                }
            }
        }

        if (ck)
            cout << bitset<4>(k) << endl;
    }

    return 0;
}

　以下の8つの演算がassociativeであることが分かりました。それぞれの関数に適当に名前を付けました。名前をつけると確かにassociativeだなあと感覚的に納得できます。この中でFSTとSNDは仲間外れの演算です。他の6つの演算と違ってcommutativeではありません。

0000	ZERO
0110	XOR
1000	AND
1001	EQ
1010	SND
1100	FST
1110	OR
1111	ONE

Introduction to Algorithms chap.2

"off in the whiteness" by angela7dreams

Chapter.2 is entitled "Getting Started."

2.1 Insertion sort

I originally had a few knowledge about sort algorithms, like bubble sort, quick sort, merge sort. But this is the first time for me to learn (or write it by myself) insertion sort. Its worst-case running time is n², but its best-case running time is n. So it's faster than other O(n²) algorithms in a particular situation, and also faster than quick sort and merge sort for sufficiently small input data. Don't know insertion sort? It's the same procedure when you sort a hand of cards.

Another important concept in this section is loop invariants, which is used to assert the termination and the correctness of algorithms. There are three types of invariants for you to consider when you evaluate an algorithm:

1. Initialization
2. Maintenance
3. Termination

2.2 Analyzing algorithms

Analyzing algorithms means analyzing the resources required and its computational time. In the book, random-access machine(RAM) is used for analysis of algorithms, where arithmetic, data movement and control take a constant amount of time. As an example, running time of insertion sort is measured, and you analyze the worse-case and the average-case running time of it.

2.3 Designing algorithms

Insertion sort is based on incremental approach. In this section, another approach called divide-and-conquer is introduced. As an example, merge sort is explained. I just implemented merge sort for a Facebook Hacker Cup problem, but the implementation in the book is better than mine. In the function MERGE() sentinels are used, and this yields a concise procedure. (Sentinel is not so much an algorithm-related thing as an implementation skill, though. I just wrote it since I was just moved by its good point.) As in "insertion sort" part, some analysis is done for merge sort.

Exercises and Problems

I'll just introduce an interesting problem.

Let A[1..n] be an array of n distinct numbers. If i < j and A[i] > A[j], then the pair (i, j) is called an inversion of A. Give a Θ(n lg n) algorithm to determine the number of inversions in A[]. (Hint: Modify merge sort.)

読書「この一言が人生を変えるイチロー思考」

　ちょっと立ち読みして気になったので買いました。イチローの思考パターンを分析した本です。野球じゃなくても何か一つにひたすらに打ち込んでいる人、何かを極めたいと思っている人にはお勧めです。

1. 嫌いな練習をどうやって毎日こなすのか
2. 結果に落ち込まない思考パターンとは
3. 目標設定の方法
4. スランプを楽しむ方法
5. 遠回りをすることが近道
6. 自分らしさの追求

などなどとても勉強になりました。

　また、ただイチローの言葉を掲載しているだけではなくスポーツ心理学の教授が分析を行っているため心理学、精神学に関するトピックがいくつか現れます。この辺りは知識として知っておいて損はないと思います。

1. 好意の返報性
2. パフォーマースキル
3. 蚤のサーカス
4. ワイナーの原因帰属理論
5. マズローの五段階欲求説

SRM 318 DIV2 1000 SimplifiedDarts

問題

ダーツをN回投げる。毎回short rangeとlong rangeを選ぶことができる。short rangeで投げて的に当たったら2点、long rangeで投げて当たれば3点もらえる。的に当たらなかった場合は0点である。short rangeで命中させられる確率はp1、long rangeで命中させられる確率はp2である。N回投げ終わった後にW点以上得点していればプレイヤーの勝ちとする。プレイヤーが勝つ確率を求めよ。

（1 <= N <= 1000, 1 <= W <= 1000）

方針

とりあえず、DPっぽいのはすぐ分かった。毎回shortにするか、longにするかプレイヤーが最適な選択をできるというのが厄介。これをどうするか。状態をdp[残りのゲーム数][今の点数]で表すと、以下の漸化式が成り立つことに気付く。

dp[N][W] = max(shortで投げた場合ゲームに勝つ確率、longで投げた場合ゲームに勝つ確率)
              = max(p1*dp[N-1][W+2] + (1-p1)*dp[N-1][W], p2*dp[N-1][W+3] + (1-p2)*dp[N-1][W])

これでやってみる。

メモ化再帰で実装

まずメモ化で書いてみた。AC。（下のソースではやってませんが、WとP1とP2は呼び出し毎に変わる変数じゃないのでメンバー変数に入れておいた方がいいです。）

double dp[1001][3001];
class SimplifiedDarts {
    double solve(int n, int p, int w, int p1, int p2) {
        if (dp[n][p] >= 0) return dp[n][p];
        if (n == 0) {
            if (p >= w) return dp[n][p] = 1.0;
            else return dp[n][p] = 0.0;
        }

        double ret = p1 / 100.0 * solve(n-1, p+2, w, p1, p2) + (100-p1) / 100.0 * solve(n-1, p, w, p1, p2);
        ret = max(ret, p2 / 100.0 * solve(n-1, p+3, w, p1, p2) + (100-p2) / 100.0 * solve(n-1, p, w, p1, p2));

        return dp[n][p] = ret;
    }

public:
    double tryToWin(int W, int N, int P1, int P2) {
        memset(dp, -1, sizeof(dp));

        return solve(N, 0, W, P1, P2) * 100;
    }
};

DPで実装

こういう時系列でみて後ろから前に詰まっていくDPは、すぐに書けないのでDPで書き直してみる。すっきりしました。

double tryToWin(int W, int N, int P1, int P2) {
    memset(dp, 0, sizeof(dp));
    FOR (i, W, 3001) dp[0][i] = 1;

    FOR (i, 1, N+1) REP(j, 3*N+1) {
        dp[i][j] = max(
                P1/100.0 * dp[i-1][j+2] + (100-P1)/100.0 * dp[i-1][j],    // short
                P2/100.0 * dp[i-1][j+3] + (100-P2)/100.0 * dp[i-1][j]     // long
                   );
    }

    return dp[N][0]*100;
}

まとめ

• 確率のDPで戦略的に次の手を選ぶことができるような問題に対して、こういうやり方はある種の定石っぽい気がする。
• DPを書くときは、base casesとSubproblem-DAGの枝の向きを意識するようにする。

Sort in Java

Played around with Java to try some sort functionalities.

What I did:

1. Just sort an integer array

2. Sort an integer array in non-increasing order

3. Sort a string array in non-decreasing order of the length

4. Sort substrings (implemented a simple suffix-array-like algorithm)

Interesting stuff:

1. Comparator is like functor in C++.

2. Anonymous class is cool! I liked this style. You can write, on the spot, an implementation of its super class (or interface).

3. Java's string data structure is clever. The way it retains strings enable to share a memory with some strings. In the code test4(), all the substrings share a memory.

4. Looks like Java Api codes are way more legible than that of C++.

Source code:

I'll post the source code below.

import java.util.Arrays;
import java.util.Comparator;

public class Test {
    public static void main(String args[]) {
        test1();
        test2();
        test3();
        test4();
    }
    
    private static void test1() {
        int xs[] = {4, 1, 4, 6, 3, 8, 10, 0};
        
        Arrays.sort(xs);
        
        System.out.println(Arrays.toString(xs));
    }
    
    private static void test2() {
        Integer xs[] = {4, 1, 4, 6, 3, 8, 10, 0};
        
        Arrays.sort(xs, new Comparator<Integer>() {
            public int compare(Integer x, Integer y) {
                return y-x;
            }
        });

        System.out.println(Arrays.toString(xs));        
    }
    
    private static void test3() {
        String names[] = {
                "hanako",
                "taro",
                "yu",
                "sho",
                "amataro",
                "takafumi"                
        };
        
        Arrays.sort(names, new Comparator<String>() {
            public int compare(String x, String y) {
                return x.length() - y.length();
            }
        });

        System.out.println(Arrays.toString(names));
    }
    
    private static void test4() {
        String text = "Oh, say can you see," +  
                      "by the dawn's early light" + 
                      "What so proudly we hailed" +
                      "at the twilight's last gleaming?" +
                      "Whose broad stripes and bright stars," + 
                      "through the perilous fight." +
                      "O'er the ramparts we watched" + 
                      "were so gallantly streaming?";
        
        String word = "gallant";
        
        // build a suffix array
        String suffix[] = new String[text.length()];
        for (int i = 0; i < text.length(); i++)
            suffix[i] = text.substring(i);
        Arrays.sort(suffix);
        
        // search the word
        int lo = 0;
        int hi = text.length() - 1;
        
        while (lo < hi) {
            int mid = (lo + hi) / 2;
            
            if (suffix[mid].compareTo(word) < 0)
                lo = mid + 1;
            else
                hi = mid;    
        }
        
        if (suffix[lo].startsWith(word))
            System.out.println(word + " is found!");
        else
            System.out.println(word + " is not found!");            
    }
    
}

読書「共喰い」

芥川賞受賞で話題になった田中慎弥さんの「共喰い」を読みました。

「共喰い 」と「第三紀層の魚」という二話が収録されています。ストーリーそのものというよりも描写や文章で魅せる作家さんなのでしょうか？いつも読むのが伊坂幸太郎なのでストーリー展開には物足りなさを感じました。

「共喰い」の方はおもしろい表現がいくつかあって、そこに深い意味があるのか意味がないのか考えるのがなかなか難しかったです。一番謎だったのは、

「便所で小便のために引っ張り出した性器は、いま見たばかりの琴子さんの首とは全然似ていない。」

という一文です。特に意味がないと言われればそれまでですが、やたらと存在感のある文章で気に成りました。あ、でも読み終わった今考えるとこれは「父親の暴力性を受け継いだ自分」と「従順な琴子さん」を表すメタファーっぽいですね。

「第三紀層の魚」は、国語の教科書に載ってる小説みたいな感じでした。国語の教科書には載せてはいけなそうな「共食い」とは対照的ですが、両作には、”田舎”、”釣り”、”家族”、”血のつながり”といった共通点がありました。

Introduction to Algorithms chap.1

I started reading a famous book entitled "Introduction to Algorithms," which is known as a textbook used in MIT. If I read one chapter a week, I would be able to finished the book in a year. Still It would take quite a long time though. Anyway I think I'm going to write memos when I'm done with a chapter.

This is about the first chapter "The Role of Algorithms in Computing." This chapter explains what the use of learning algorithms. I found an interesting question in this chapter.

"Suppose computers were infinitely fast and computer memory was free. Would you have any reason to study algorithms?"

The answer is, of course, yes! (Truth be told, I was not able to find a witty answer by myself..)

You still want to know:

1. Your algorithm terminates?

2. If so, with a correct answer?

It also mentions quite a few areas in which algorithms really help.

• hardware design
• graphical user interface
• networking
• computer language (compiler, interpreter, or assembler)

Some people say, "In this age when the computer has developed this far in a sense of hardware, what the use of learning fast algorithm?" But as the book says, "With the ever-increasing capacities of computers, we use them to solve larger problems than ever before."

I would conclude that this first chapter is really encouraging for those who want to start learning algorithms. You should try it out.

Facebook Hacker Cup 2012 Round2

1SUBMIT/1WAというひどい結果でした。自分の今の実力でTop100に入れるなんて思ってないし、もっと練習しなければと思いました。とりあえず復習してAとBは解けたので簡単な解説を書きます。

Road Removal

先に重要じゃない都市同士を結ぶ道路をすべて採用します。するとグラフが、重要じゃない都市のみで構成される複数の連結成分と複数の重要な都市から成り立つ森になります。前者の連結成分を一つの節点とみなしてクラスカル法のようなことをすればOK。使用するアルゴリズムや実装は簡単だけどどのアルゴリズムを適用すれば良いのかが見えにくいという問題で、個人的には良問だと思います。

const int MAX = 10000;
int par[10000];
int rank[10000];

void init(int n) {
    REP(i, n) {
        par[i] = i;
        rank[i] = 0;
    }
}

int find(int x) {
    if (x == par[x])
        return x;
    return par[x] = find(par[x]);
}

bool same(int x, int y) {
    return find(x) == find(y);
}

void merge(int x, int y) {
    x = find(x);
    y = find(y);

    if (x == y)
        return;
    if (rank[x] > rank[y]) {
        par[y] = x;
    } else {
        par[x] = y;
        if (rank[x] == rank[y])
            rank[y]++;
    }
}

void solve() {
    int T;

    scanf("%d", &T);
    REP(t, T) {
        int N, M, K;

        scanf("%d %d %d", &N, &M, &K);
        init(N);

        int a, b;
        vector<pair<int, int> > road;
        REP(i, M) {
            scanf("%d %d", &a, &b);
            if (min(a, b) >= K)
                merge(a, b);
            else
                road.push_back(MP(a, b));
        }

        int ret = 0;
        REP(i, road.size()) {
            a = road[i].first;
            b = road[i].second;

            if (same(a, b))
                ++ret;
            else
                merge(a, b);
        }

        printf("Case #%d: %d\n", t+1, ret);
    }
}

Monopoly

Union Findと動的計画の合わせ技です。dp[i][j]に会社iの社長が直属の部下をj人持つときの木の高さの最小値を保持します。あとポイントとなるのは、dp[i][j]の更新を高速に計算するためにminHeight[i]に現時点における会社iが取り得る木の高さの最小値を保存しておくことです。Union Findの一度の操作をO(log(N))とすると、一つの問題はO(N log(N) + ND)で計算できます。

const int INF = 999999999;
const int MAX_N = 30000;
const int MAX_D = 5000;
int dp[MAX_N][MAX_D+1];
int minHeight[MAX_N];
int par[MAX_N];
int rank[MAX_N];

void init(int n) {
    REP(i, n) {
        par[i] = i;
        rank[i] = 0;
    }
}

int find(int x) {
    if (x == par[x])
        return x;
    return par[x] = find(par[x]);
}

void merge(int x, int y) {
    x = find(x);
    y = find(y);

    if (x == y) return;
    if (rank[x] > rank[y])
        par[y] = x;
    else {
        par[x] = y;
        rank[y]++;
    }
}

bool same(int x, int y) {
    return find(x) == find(y);
}

void solve() {
    int T;
    scanf("%d", &T);

    REP(t, T) {
        int N, D;
        scanf("%d %d", &N, &D);

        init(N);
        REP(i, N) REP(j, D+1) dp[i][j] = INF;
        REP(i, N) {
            minHeight[i] = 1;
            dp[i][0] = 1;
        }

        int a, b;
        REP(i, N-1) {
            scanf("%d %d", &a, &b);
            a = find(a-1);
            b = find(b-1);

            merge(a, b);
            int x = find(a);
            dp[x][0] = INF;
            for (int j = D; j > 0; j--)
                dp[x][j] = min(max(dp[a][j-1], 1+minHeight[b]),   // a becomes the president
                               max(dp[b][j-1], 1+minHeight[a]));  // b becomes the president

            minHeight[x] = INF;
            REP(j, D+1)
                minHeight[x] = min(minHeight[x], dp[x][j]);
        }

        int ret = INF;
        int x = find(0);
        REP(i, D+1)
            ret = min(ret, dp[x][i]);

        printf("Case #%d: %d\n", t+1, ret);
    }
}

Javaで文字列の変更

Javaのメモ。「Stringで渡された文字列をある条件を満たすように回文にしてStringで返せ」という問題があって、文字列の一部を変更したい場合どうするんだっけ？となったので、いくつかやってみた。

1. char[]に変換して特定の文字を更新、その後Stringオブジェクトに戻す
2. byte[]に変換して特定の文字を更新、その後Stringオブジェクトに戻す
3. StringBufferを使う
4. Stringbuilderを使う

まず、1.のやり方。簡単のため、"hogehoge2011"を"hogehoge2012"にする場合を考えます。

public static void main(String args[]) {
    String hoge = "hogehoge2011";
    
    char []chrs = hoge.toCharArray();
    chrs[chrs.length-1] = '2';
    hoge = new String(chrs);
    
    System.out.println(hoge);
}

char[]からStringに戻すときは、Stringコンストラクタにchar[]を渡してあげます。

hoge = chrs.toString();

や、

hoge = Arrays.toString(chrs);

を使ってしまいそうになりますが、間違いです。前者は、ObjectクラスのtoString()が呼ばれ「オブジェクトの派生元のクラス名、アットマーク (@)、およびオブジェクトのハッシュコードの符号なし 16 進表現から構成される文字列」を返します。こんなのがhogeに代入されます。

[C@10b30a7

また、後者のArrays.toString(chr)の場合は、以下のような文字列がhogeに代入されます。

[h, o, g, e, h, o, g, e, 2, 0, 1, 2]

ということで、char[]からStringにC++のような代入をしたい場合は、Stringのコンストラクタを使うようです。

2.は1.と同様です。Javaのcharは2バイトの領域を持っています。これに対してbyteは1バイトなので、文字コードが1バイトに収まる文字だけが対象の場合は、byte[]で扱った方が効率的です。

3. StringBufferオブジェクトを利用したやり方です。

    public static void main(String args[]) {
        String hoge = "hogehoge2011";
        
        StringBuffer sb = new StringBuffer(hoge);
        sb.setCharAt(sb.length()-1, '2');
        hoge = sb.toString();
        System.out.println(hoge);
    }

4. StringBuilderを利用したやり方は、StringBufferの場合と同様なので省略します。両者の違いが気になりますが、以下のような違いがあります。

• 提供する機能は同じ
• StringBuilderは高速だが、同期を保証しない
• StringBufferは同期を保証するが、低速

ということで、可能な場合はStringBuilderの使用が推奨されています。

オイラーの多面体定理

球面と同相な多面体の頂点の数をV、辺の数をE、面の数をFとすると以下の関係が成り立ちます。

　　　V + F - E = 2

ここのページの説明が分かりやすかったです。

http://homepage3.nifty.com/sugaku/tamentaisyomeians.htm

説明の概略は以下のとおり。

1. 多面体の一つの面を取り外して平面に押しつぶして平面グラフを作る。
2. グラフが木になるまで、枝をとりのぞいていく。（枝を1つ減らすと面の数も1つ減るのでV+F-Eは不変）
3. 木の場合は、V+F-E=2が分かっている。

外側の無限の広さを持った空間も一つの面として考えることで、取り外した面との整合性をとっているのが面白いと思いました。

　上記のページにはもう一つ面白い関係が紹介されていました。任意の平面グラフにおいて

　　　2E ≧3F

が成り立つ。

この説明が分かりづらかったので調べてみました。以下のページの説明が分かりやすいかったです。

　http://www-math.mit.edu/phase2/UJM/vol1/EFEDUL~1.PDF

V=2, E=1の連結グラフの場合は上の関係は成り立たないので、正しくは「V≧3の連結な平面グラフ」という条件のもと、

　　　2E ≧3F

が成り立つ。です。

証明の概略は以下のようになります。まず大きくi)平面グラフGの辺の数が3未満の場合、ii) それ以外の場合で場合分けします。

i)のとき、V≧3という条件と合わせると、V=3、E=2、F=1の場合しかありえません。このとき、2E > 3Fなので成り立つ。

ii)のとき、すべての面において境界となる辺の数の和（以下ではSum(|e(f)|)と書きます。）を考えます。ある面の境界となる辺の数は3以上です。（ii)の条件より無限に広がる外側の面の境界辺の数も3以上であることに注意。）面はF個あるので、Sum(|e(f)|)は3F以上です。

次に辺の観点から考えます。一つの辺は多くても面の境界として数えられるのは2回だけです。（一つの辺が3つ以上の面の境界とは成りえないから。）よって、Sum(|e(f)|)は2E以下です。

以上から、2E ≧ Sum(|e(f)|) ≧3Fとなります。

等号成立は、すべての枝が2つの面の境界となっていて、かつ、すべての面が3辺によって境界づけられる場合なので、V=3のときの完全グラフだけかと思います。参照元のページには"equality holds if and only if every face is a triangle."とありましたが、三頂点の完全グラフ意外にそれを満たすグラフってあるんでしょうか。。