ペル方程式を解く

　Pythonでペル方程式を解くプログラムを書きました。
ペル方程式とはディオファントス方程式の一つで以下のような形をしているものです。

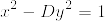
解き方

ペル方程式を変形すると、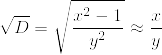

となります。よって、Dの平方根の有理数近似をx/yとすると、（x, y）が解の候補となりそうです。
有理数近似には、連分数展開が使えそうです。
実際に、ペル方程式の解を(x, y)とすると、x/yは√Dのconvergentとなる[1]ことが証明できます。よってconvergentを列挙し、方程式を満たすかどうか調べれば不足なくペル方程式の解を求めることが出来ます。

上の計算手続きで方程式の解を求めることができますが、コンピュータを使って計算する場合は注意点があります。
浮動小数点演算を使って平方根の連分数展開を行うと誤差が大きくなってしまい、正しい結果が得られないということです。これを回避するために、整数演算のみで平方根の連分数展開を行う方法が知られています[2]。

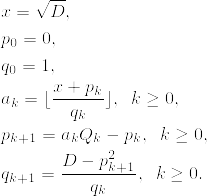
とすると、[a0; a1, a2, a3, ...]が√Dの連分数展開となります。

プログラム

D=2の場合のペル方程式を解いています。解を10個列挙しています。

import itertools

# check if x^2 - D y^2 = k holds.
def check_pell_equation(D, k):
    def f(x, y):
        return x * x - D * y * y == k
    return f

# calculate the continued fraction of the square root of d.
def continued_fraction_of_sqrt(d):
    p, q = 0, 1
    x = int(d ** 0.5)

    while True:
        a = (x + p) / q
        yield a
        p = a * q - p
        q = (d - p * p) / q

# solve a Pell's equation x^2 - D y^2 = k, 
#  where D is a non-square number, k is +1 or -1.
def solve_pell_eqation(D, k):
    pell_eq = check_pell_equation(D, k)
    cf = continued_fraction_of_sqrt(D)
    
    p0, q0 = 0, 1
    p1, q1 = 1, 0

    while True:
        if pell_eq(p1, q1):
            yield p1, q1
        a = cf.next()
        p1, p0 = a * p1 + p0, p1
        q1, q0 = a * q1 + q0, q1

if __name__ == '__main__':
    ret = solve_pell_eqation(2, 1)
    
    for x, y in itertools.islice(ret, 10):
        print x, y

参考

[1] Solution of Pell's Equation is a Convergent
[2] c++ - Generating continued fractions for square roots - Stack Overflow
[3] MathForKids Pell's Equation (YouTube Video)