計算量は、(行数 4) * (カラムの埋まっている文字 50^2) * (現在注目している行の文字の分割パターン 50^2) * (文字列比較 50)であやしかったけど、投げてみる。TLE。ループの中にbreakを入れて枝狩りをしてみる。Accept。
んー、通ったものの、計算量はもう一段階落ちると思う。文字列の比較をハッシュとか使ってやればいいのかなー。Editorialに期待します。
long long int dp[4][51][51];
class MagicalSquare {
public:
long long int getCount(vector<string> rowStrings, vector<string> columnStrings) {
memset(dp, 0, sizeof(dp));
vector<string> rows(4);
rows[0] = "";
REP(i, rowStrings.size()) rows[i+1] = rowStrings[i];
dp[0][0][0] = 1;
int rLen[4];
int cLen[3];
REP(i, 4) rLen[i] = rows[i].length();
REP(i, 3) cLen[i] = columnStrings[i].length();
if (rLen[1] + rLen[2] + rLen[3] != cLen[0] + cLen[1] + cLen[2])
return 0;
int s = 0;
REP (r, 3) {
s += rLen[r];
REP (i, cLen[0]+1) REP(j, cLen[1]+1) {
if (!dp[r][i][j]) continue;
int k = s - i - j;
REP(p, rLen[r+1]+1) {
string s1 = rows[r+1].substr(0, p);
if (columnStrings[0].substr(i, s1.length()) != s1) break;
FOR (q, p, rLen[r+1]+1) {
string s2 = rows[r+1].substr(p, q-p);
string s3 = rows[r+1].substr(q);
if (columnStrings[1].substr(j, s2.length()) != s2) break;
if (columnStrings[2].substr(k, s3.length()) != s3) continue;
dp[r+1][i+s1.length()][j+s2.length()] += dp[r][i][j];
}
}
}
}
return dp[3][cLen[0]][cLen[1]];
}
};



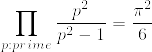
%7D.png)
%20%3D%20%5Cprod_%7Bp%20:%20prime%7D%20%5Cfrac%7Bp%5Ex%7D%7Bp%5Ex%20-%201%7D.png)
