ζ(2) = π2 / 6の証明を読んでいて、ふとsin(x)のテイラー展開について気になった。0の周りでテイラー展開するとして、例えば x = 100くらいでもそれなりの精度で近似するためにはどれくらいの項数がいるのだろうか。
sin(x)は周期関数なので、[0, 2π)に入るようにxを変換すれば、x = 2πのときにどれだけ項数が必要か考えれば十分だと思うけど、周期性は利用しないという前提で。
x < 1であれば、xk → 0になるので高次の項は無視できるというのはすぐに分かるけど、x > 1のときって高次の項は無視できるのだろうか?
xk/k! を考えると、kが大きくなるにつれ、分子の増加よりも分母の増加の方が速くなるため、x > 1のときも十分に大きなkを取れば、xk/k! → 0 になりそうである。じゃあ十分に大きなkってどれくらいだろうか?スターリングの公式が使えそうな気がする。
k! ~ (k/e)kなので、
xk/k! ~ xk/((k/e)k) = (ex/k)k
である。
これを使って、0 <= x < 100にてsin(x)をテイラー展開近似するのに必要な項数を見積もってみる。
大事なことを書き忘れていた。sin関数のテイラー展開は以下のようになる。
sin(x) = 1 - x3/3! + x5/5! - x7/7! + x9/9! - ....
x = 100として、xk/k! ~ (ex/k)k < 10-6となるようなkを概算してみる。
k = 300のとき、(ex/k)k = 1.42 * 10-13なので、300/2 = 150項あれば十分なのではないかと予想してみる。
以下に、[0, 100]でのsin関数とそのテイラー展開近似(150項まで)をグラフにしてみた。十分な近似ができているようだ。
Search on the blog
2014年10月30日木曜日
2014年10月28日火曜日
1+2+3+4+5+ ..... = -1/12
最近摩訶不思議な式に出くわした。
1 + 2 + 3 + 4 + ..... = -1/12らしい。
詳しいことは分からないが、様々な物理の分野で使用される式らしい。
S = 1 + 2 + 3 + 4 + ......
S1 = 1 - 1 + 1 - 1 + 1 ....
S2 = 1 - 2 + 3 - 4 + 5 ....
と定義する。
まず、
1 - S1 = 1 - (1 - 1 + 1 - 1 ....) = S1より、 2S1 = 1となる。
よってS1 = 1/2が成り立つ。
次に、
S2 = 1 - 2 + 3 - 4 + 5 ....
S2 = 1 - 2 + 3 - 4 + 5 ....
として(下段のS2が1項右にずれているのがポイント)、両辺を足すと、
2S2 = 1 - 1 + 1 - 1 + 1 .... = S1より、
2S2 = 1/2となる。よって、S2 = 1/4が導かれる。
最後に、
S = 1 + 2 + 3 + 4 + .....
S2 = 1 - 2 + 3 - 4 + .....
として上段から下段の式を引くと、
S - S2 = 4 + 8 + 12 + 16 + ... = 4Sより、3S = - S2となる。
よって、S = -1/12である。
1 + 2 + 3 + 4 + ..... = -1/12らしい。
詳しいことは分からないが、様々な物理の分野で使用される式らしい。
証明
S = 1 + 2 + 3 + 4 + ......
S1 = 1 - 1 + 1 - 1 + 1 ....
S2 = 1 - 2 + 3 - 4 + 5 ....
と定義する。
まず、
1 - S1 = 1 - (1 - 1 + 1 - 1 ....) = S1より、 2S1 = 1となる。
よってS1 = 1/2が成り立つ。
次に、
S2 = 1 - 2 + 3 - 4 + 5 ....
S2 = 1 - 2 + 3 - 4 + 5 ....
として(下段のS2が1項右にずれているのがポイント)、両辺を足すと、
2S2 = 1 - 1 + 1 - 1 + 1 .... = S1より、
2S2 = 1/2となる。よって、S2 = 1/4が導かれる。
最後に、
S = 1 + 2 + 3 + 4 + .....
S2 = 1 - 2 + 3 - 4 + .....
として上段から下段の式を引くと、
S - S2 = 4 + 8 + 12 + 16 + ... = 4Sより、3S = - S2となる。
よって、S = -1/12である。
参考URL
[1] ASTOUNDING: 1 + 2 + 3 + 4 + 5 + ... = -1/12
2014年10月5日日曜日
ペル方程式を解く
Pythonでペル方程式を解くプログラムを書きました。
ペル方程式とはディオファントス方程式の一つで以下のような形をしているものです。
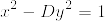
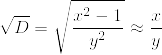
となります。よって、Dの平方根の有理数近似をx/yとすると、(x, y)が解の候補となりそうです。
有理数近似には、連分数展開が使えそうです。
実際に、ペル方程式の解を(x, y)とすると、x/yは√Dのconvergentとなる[1]ことが証明できます。よってconvergentを列挙し、方程式を満たすかどうか調べれば不足なくペル方程式の解を求めることが出来ます。
上の計算手続きで方程式の解を求めることができますが、コンピュータを使って計算する場合は注意点があります。
浮動小数点演算を使って平方根の連分数展開を行うと誤差が大きくなってしまい、正しい結果が得られないということです。これを回避するために、整数演算のみで平方根の連分数展開を行う方法が知られています[2]。
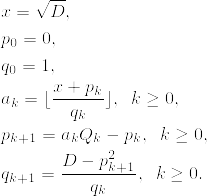
とすると、[a0; a1, a2, a3, ...]が√Dの連分数展開となります。
[2] c++ - Generating continued fractions for square roots - Stack Overflow
[3] MathForKids Pell's Equation (YouTube Video)
ペル方程式とはディオファントス方程式の一つで以下のような形をしているものです。
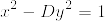
解き方
ペル方程式を変形すると、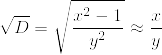
となります。よって、Dの平方根の有理数近似をx/yとすると、(x, y)が解の候補となりそうです。
有理数近似には、連分数展開が使えそうです。
実際に、ペル方程式の解を(x, y)とすると、x/yは√Dのconvergentとなる[1]ことが証明できます。よってconvergentを列挙し、方程式を満たすかどうか調べれば不足なくペル方程式の解を求めることが出来ます。
上の計算手続きで方程式の解を求めることができますが、コンピュータを使って計算する場合は注意点があります。
浮動小数点演算を使って平方根の連分数展開を行うと誤差が大きくなってしまい、正しい結果が得られないということです。これを回避するために、整数演算のみで平方根の連分数展開を行う方法が知られています[2]。
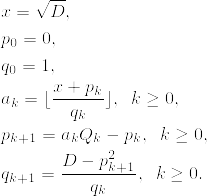
とすると、[a0; a1, a2, a3, ...]が√Dの連分数展開となります。
プログラム
D=2の場合のペル方程式を解いています。解を10個列挙しています。
import itertools # check if x^2 - D y^2 = k holds. def check_pell_equation(D, k): def f(x, y): return x * x - D * y * y == k return f # calculate the continued fraction of the square root of d. def continued_fraction_of_sqrt(d): p, q = 0, 1 x = int(d ** 0.5) while True: a = (x + p) / q yield a p = a * q - p q = (d - p * p) / q # solve a Pell's equation x^2 - D y^2 = k, # where D is a non-square number, k is +1 or -1. def solve_pell_eqation(D, k): pell_eq = check_pell_equation(D, k) cf = continued_fraction_of_sqrt(D) p0, q0 = 0, 1 p1, q1 = 1, 0 while True: if pell_eq(p1, q1): yield p1, q1 a = cf.next() p1, p0 = a * p1 + p0, p1 q1, q0 = a * q1 + q0, q1 if __name__ == '__main__': ret = solve_pell_eqation(2, 1) for x, y in itertools.islice(ret, 10): print x, y
参考
[1] Solution of Pell's Equation is a Convergent[2] c++ - Generating continued fractions for square roots - Stack Overflow
[3] MathForKids Pell's Equation (YouTube Video)
登録:
コメント (Atom)
